Proiezioni cartografiche e
punto di vista (scheda
2-2)
È chiaro fin dal titolo che questo è un argomento che esula
totalmente dalle possibilità di astrazione dei bambini e che quindi deve
essere affrontato come un gioco, senza alcuna attinenza ad applicazioni
pratiche.
Il problema "geografico" (cioè geometrico) si pone in questi termini: se
abbiamo una regione (o un continente) adagiato sulla superficie
sferica terrestre e se vogliamo proiettare questa regione su uno schermo
piano - tangente o esterno alla sfera - dobbiamo definire un "punto di
vista" e quindi la posizione di un osservatore che guarda la regione e
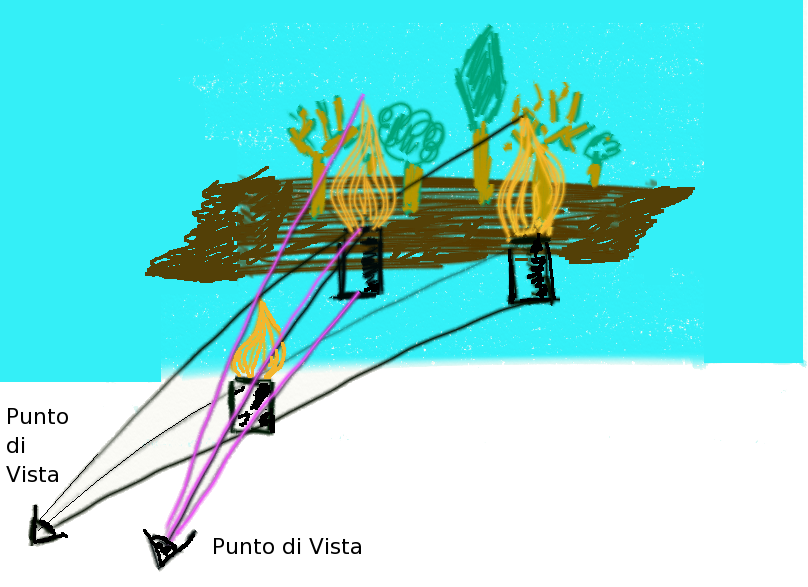
la vede proiettata sul piano. È ovvio che la posizione
dell'osservatore modifica - a seconda dei casi - la posizione e/o la forma
della figura proiettata, come ad esempio si vede nella figura successiva,
nella quale non si è tenuto conto della variazione della distanza relativa
tra osservatore e oggetto da proiettare.
Lo stesso effetto si ha, ad esempio, quando si misura una temperatura
con un termometro in cui il mercurio è distante dalla scala: la posizione
dell'occhio dell'osservatore o, come si dice, la parallasse, può
modificare la lettura del termometro.
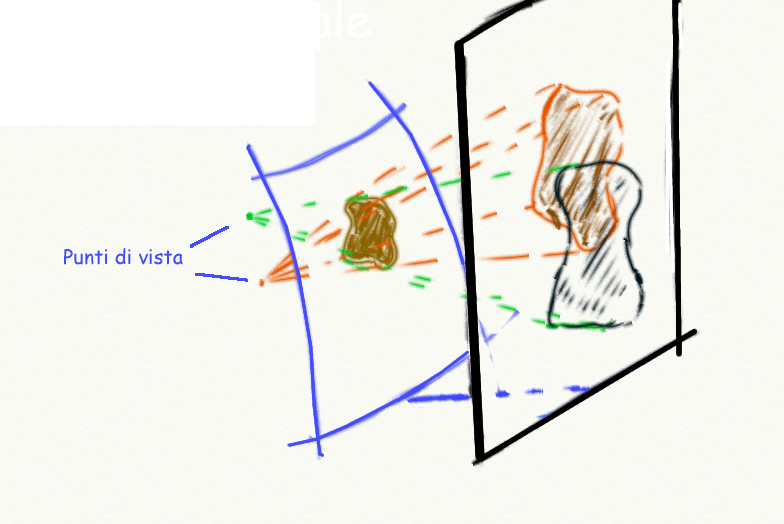
La proiezione azimutale si presenta in questo modo se il piano di
proiezione NON è tangente alla Terra e se i diversi "punti di vista" sono
allineati lungo il diametro perpendicolare al piano su cui si proietta.
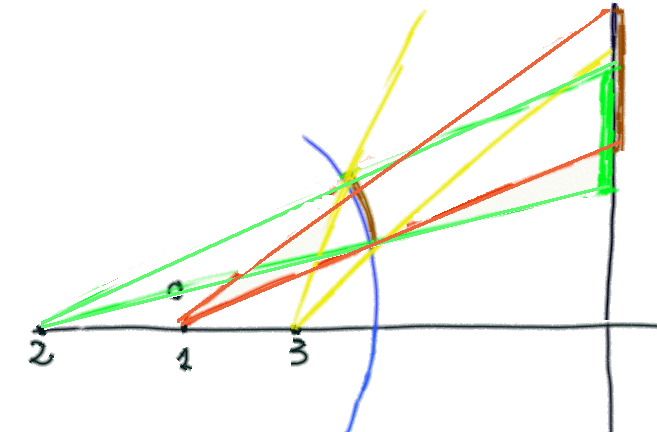
oppure in questo, se il piano è tangente alla Terra e perpendicolare alla retta
passante per il centro:
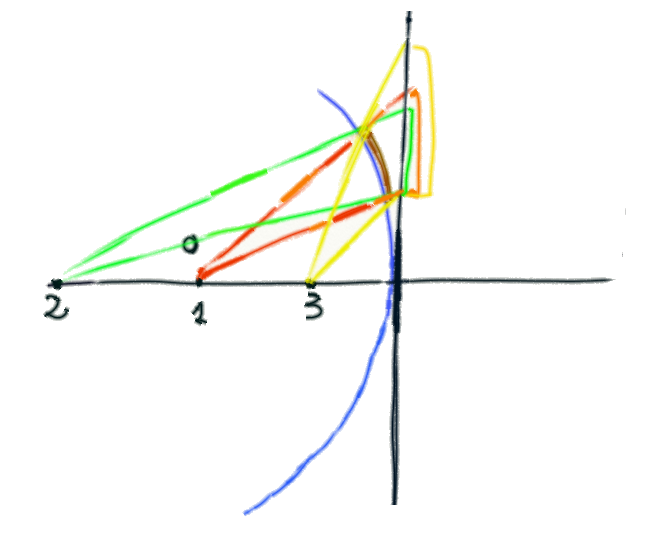
La proiezione obliqua, cioè quando la perpendicolare al piano che passa
per il centro della Terra non coincide con l'equatore, mostra come si
possano ottenere grandi deformazioni della stessa regione. Le
deformazioni di una proiezione azimutale dipendono dalla posizione
dell'osservatore.

Ora, l'osservatore è chi "proietta" l'immagine reale sullo
schermo: in un esperimento semplificato il suo posto può essere preso da
una lampada (il più possibile puntiforme per evitare le ombre non nitide)
che proietta sulla parete l'ombra di un oggetto di forma regolare (una
tavoletta quadrata o triangolare, un piattino, un elemento delle
costruzioni, ecc).
Dopo aver giocato con le ombre per un po' ed averle riprodotte su un
foglio appoggiato alla parete, ci si può chiedere se è possibile "prevedere" le
deformazioni e su questo si può organizzare un gioco secondo i normali
schemi ludici della sezione.
Forse questo è un gioco al quale potrebbero partecipare le 3 fasce di
età: lo scopo è quello di far toccare con mano che la proiezione
deforma e che le immagini proiettate su uno schermo hanno sempre
qualcosa di diverso rispetto all'originale.
In sezione si può organizzare una dimostrazione su come si comporta
l'ombra (cioè l'immagine proiettata) al cambiare della posizione della
lampada (cioè del punto di vista). Qualcosa di simile a quanto descritto nel
disegno successivo, ricordando che forse è bene lasciare inalterata la
posizione della figura da proiettare, per non complicare troppo la
situazione logistica.
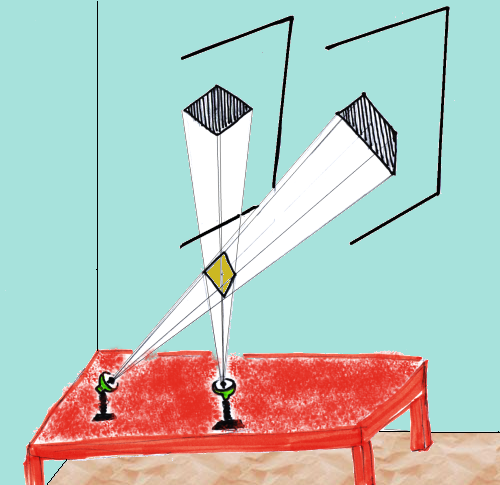
Se fosse necessario si può ricalcare l'ombra prodotta in una posizione
della lampada e appoggiare il disegno sulla seconda ombra, in modo da
confrontare le dimensioni e le forme.
Nella discussione che dovrebbe seguire le fasi osservativa e ludica si
cercherà di mettere in evidenza
- che i cambiamenti di dimensione dipendono
dalla distanza della lampada dall'oggetto. L'oggetto, però, è fisso e la sua
posizione non dovrebbe entrare nella discussione, almeno nelle prime fasi.
Solo in un secondo momento si potrà tenere fissa la lampada e muovere
l'oggetto, cercando di mostrare come l'unica cosa che conta è la posizione
relativa tra la lampada e l'oggetto (in realtà conta anche la posizione
dello schermo rispetto a lampada e oggetto, ma per semplicità supponiamo
all'inizio di non introdurre questa terza variabile) e non la loro posizione assoluta;
- che i cambiamenti di forma (deformazioni) dipendono dall'angolo sotto il
quale l'oggetto "viene visto" dall'occhio (cioè dalla lampada). Questo
angolo, misurato su una scala orizzontale, viene detto azimut.
- Se la situazione logistica lo consente, è possibile sfruttare il moto
del sole per segnare, marcare, in sezione, le zone di buio e quelle di luce,
per osservare i cambiamenti nel tempo e per sottolineare la ciclicità
(cioè il ritorno alla stessa situazione giorno dopo giorno) del moto
apparente del sole.
Relativamente a questa parte, quanto viene puntualizzato in sezione
può essere successivamente applicato
all'esterno, quando la stagione diventa adatta alle uscite, come
osservazione delle ombre e loro ricalco con gesso o sassolini e come
osservazione dei cambiamenti delle forme man mano che il sole si muove.
Ad esempio, con un'applicazione del tipo di quella mostrata nelle tre foto
successive, realizzata in una scuola dell'infanzia:
foto1
foto2
foto3
Questo tipo di attività sarà propedeutica ad ogni successivo (alla scuola
primaria e alla media) studio delle proiezioni cartografiche e
geometriche.
Pagina scritta il 21.2.06. Ultimo aggiornamento: 26.2.12






