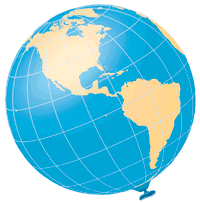
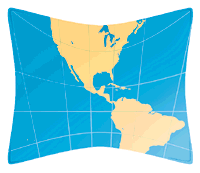
Le proiezioni cartografiche

Il problema che deve affrontare chi disegna le carte geografiche consiste nel trovare un accorgimento per rappresentare una superficie sferica (la Terra) su un foglio piano (la carta geografica). Il problema non si pone quando si vogliono rappresentare piccolissime porzioni di superficie terrestre (per esempio le carte catastali), ma diventa notevole quando le aree da rappresentare sono molto grandi. Si parla allora di proiezioni cartografiche, cioè di un insieme di regole che permettono di riportare sul piano della carta ogni punto della superficie terrestre rappresentata.
Non è possibile spianare una superficie sferica o, più in generale curva, senza deformarla, cioè senza apportare compressioni ed espansioni ad alcune, se non a tutte le sue parti.
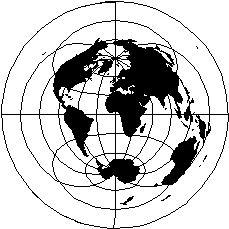
La proiezione di Mercatore, per esempio, fa aumentare le aree procedendo dall'equatore verso i poli. Nella figura lo spicchio contenente la Groenlandia si proietta in un rettangolo che, all'equatore si confonde con la corrispondente superfice della sfera, ma ai poli aumenta enormemente la superficie proiettata di questa penisola.
Proiezioni diverse, nella stessa scala e rappresentanti la stessa area, vengono così a non essere sovrapponibili e questo tanto più quanto più ci si allontana dal centro di proiezione. Nella figura sono state sovrapposte tre proiezioni degli Stati uniti, aventi lo stesso centro; notate che, lontano da esso, le differenze sono notevoli, tali da dar luogo a tre rappresentazioni ben separate della penisola della Florida.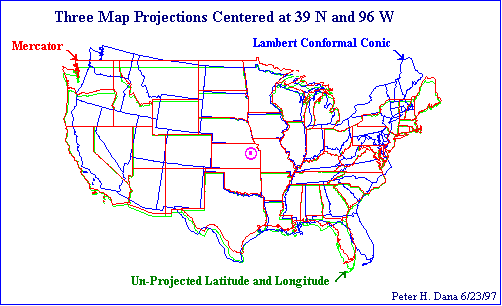

Si può però scegliere quali distorsioni introdurre e quali proprietà conservare.

Proiezione azimutale equidistante
 Il cartografo può voler conservare in scala tutte le distanze che intercorrono tra i luoghi della regione rappresentata, in questo caso la proiezione si chiama equidistante: il rapporto tra due distanze sulla carta è uguale al rapporto tra le corrispondenti distanze nella realtà.
Generalemte solo le carte topografiche, con rapporto di scala 1:25.000 od inferiore, sono equidistanti; nelle proiezioni a scala maggiore l'equidistanza si mantiene solo lungo una determinata direzione. Un esempio di proiezione equidistante è la proiezione azimutale equidistante
Un'altra utile proprietà è l'equivalenza; nelle proiezioni equivalenti, si conservano le aree: due superfici sulla carta stanno nello stesso rapporto che intercorre tra le corrispondenti superfici nella realtà. Per le latitudini intermedie la proiezione sinusoidale realizza l'equivalenza.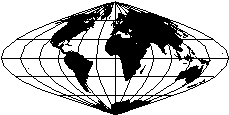
Proiezione sinusoidale
Proiezione del Mercatore
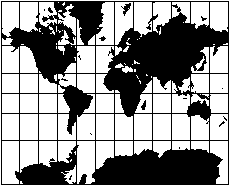
 Nelle proiezioni isogone o conformi si conservano gli angoli tra due direzioni qualsiasi e quindi vengono mantenute le forme degli oggetti rappresentati.

La proiezione di Mercatore è una proiezione conforme: forme e direzioni sono corrette, ma non certo le aree. Si noti che in questa proiezione paralleli e meridiani si incontrano formando angoli retti, come nella realtà.

Quando si ha la necessità di rappresentare grandi aree o addirittura l'intero globo vengono utilizzate delle proiezioni modificate, in modo da minimizzare le distorsioni e conservare il più possibile tutte le proprietà. Una di queste e' la proiezione di Robinson.
Proiezione di Robinson

Un'altra interessante proprietà, molto utile nella navigazione, è data dalla rappresentazione delle linee ortodromica e lossodromica:

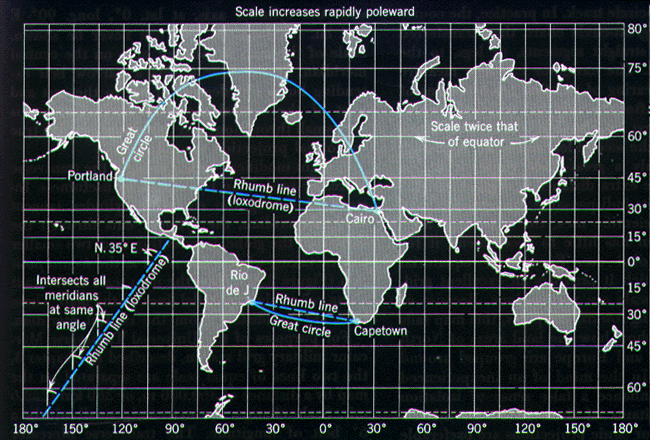
Nella proiezione di Mercatore la lossodromica è una linea retta e l'ortodromica una linea curva.

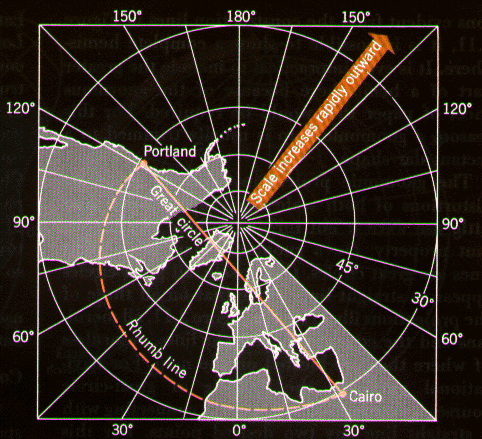
Nella proiezione gnomonica polare invece, l'ortodromica è una linea retta e la lossodromica una linea curva.

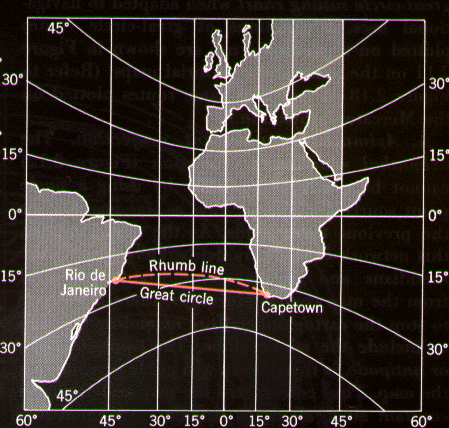
Anche nella proiezione gnomonica equatoriale, l'ortodromica è una linea retta e la lossodromica una linea curva.

Dobbiamo la gran parte delle immagini usate in questa pagina a Peter H. Dana, docente presso il Department of Geography, University of Texas at Austin che è autore di interessanti lezioni sull'argomento all'indirizzo:

Altri siti interessanti in rete: